Abstract:
Quantum electrodynamics suggests that the vacuum is a multi-dimensional
realm stressed with an extremely high potential known as the zero-point
energy. Recent crystallographic studies have yielded an interesting geometry
that may be an indicator of how dimensionality enfolds within this active
vacuum.
The earliest theories of light relied upon the existence of an æther, a rarefied gas-like medium of propagation, to explain the transmission of light over distance. Light was theorized to be analogous to sound, consisting of longitudinal (one-dimensional) waves. Each photon in this model is a soliton, or solitary wave. Such theories of light were abandoned early in this century due to experimental failure to conclusively detect the existence of such an æther.
Something very similar to an æther is to be found in the world of quantum electrodynamics, which views the vacuum as being far from empty. Both theory and experimental observation suggest that the fabric of space is a turbulent plasma-like realm comprised of virtual particles continuously appearing from and disappearing into a physical hyperspace. This virtual particle flux has an enormous energy density, the "zero point energy", of about 1093 g/cm3.1 It is termed zero-point because the motion imparted by the virtual particle flux is not thermal in nature and is present even at the "zero-point" of zero degrees Kelvin, where all atomic motion is supposed to stop.
Investigators attempting to interact with this hyperdimensional "æther" will probably need to establish some type of resonant system. There have been a number of interesting proposals for doing this, and the most promising among them would produce oscillation of ions in a plasma. Moray B. King describes the positive ions in a plasma as being capable of "polarizing" the vacuum, that is, establishing coherent lines of zero-point energy flux directly from the hyperspace where the zero-point energy resides.2 There has also been speculation that a rotating mass, particularly one bearing a high electrostatic charge, will produce vacuum polarization along with gravitational and inertial anomalies.3
The Quasicrystal experiment
In 1984, researchers at the National Institute of Standards and Technology dropped a molten alloy of aluminum and manganese onto the surface of a rapidly spinning wheel. The purpose of the spinning wheel was to solidify the molten metal as rapidly as possible so as to observe the effects that rapid cooling would have on the sample. The crystalline structure of the resulting solid was quite unexpected.4
Crystallographic analysis showed that many of the samples had an icosahedral lattice structure in violation of the rules of classical crystallography, hence the name "quasicrystal". Mathematicians studying this lattice structure made an important observation: the icosahedral symmetry could be replicated mathematically by taking a cut through a regular six-dimensional lattice. Thus, the laws of classical crystallography which require regular lattices are satisfied by viewing icosahedral crystals as 3-D hypersurfaces in 6-D space.5
If the process for forming the quasicrystals produced a vacuum polarization with a hyperdimensional æther, we may then speculate that the solidified quasicrystal might bear a "frozen" hyperspatial pattern recording this vacuum polarization event.
Complexified Three-Space
If the icosahedral quasicrystal symmetry is indicative of how dimensionality enfolds in the vacuum state, then there should be some relationship between the icosahedron and higher dimensional spaces. The icosahedron does have such a relation, and it involves a polytope, or higher-dimensional polyhedron, described early in this century by the Canadian geometer H. S. M. Coxeter. It is called Polytope 2,21.6
Polytope 2,21 is described by Coxeter as consisting of 27 points that are evenly distributed over the surface of a 5-D sphere in six-dimensional space. There are two forms apparently isomorphic with polytope 2,21 that may have relevance to the study of vacuum geometry.
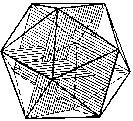
One method was suggested by Stan Tenen of the Meru Foundation. Three Golden Section rectangles are placed mutually orthogonal to one another. The corners of these rectangles will mark the vertices of an icosahedron. (See Figure 1) The planes themselves are extensions of the three coordinate axes: X, Y, and Z. For each direction, the one-dimensional line has been orthorotated into a two dimensional plane. This orthorotation is similar to the graphic description of complex numbers, numbers of the form a + bi, where a and bi are termed the real and imaginary components. The real and imaginary components of complex numbers are usually depicted together as a two-dimensional plane.
Figure 1.
Three Mutually Orothogonal Complex Planes
Form an Icosahedron
(From The Divine Proportion, by H.E. Huntley; 1970,
Dover)
So each Golden Section rectangle that forms this icosahedron may be thought of as a complex plane, and as there are three of them, they give us a way of representing a six-dimensional space. Since each dimension, X, Y, and Z, is being simultaneously orthorotated to a higher dimensionality, we can refer to the result as complexified three-space. It is an immediate jump from 3-D to 6-D. The 27 points of polytope 2,21 can now be evenly distributed as nine points on each rectangle, with each set of nine arranged in a Fibonacci spiral.
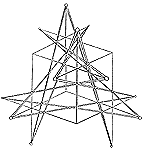
Figure 2.
The Schlafli Double-Six
(From Geometry and the Imagination,
by D. Hilbert & S. Cohn-Vossen, 1952, Chelsea)
Another way to project polytope 2,21 into three-space is to make use of Coxeter's observation that the 27 points on the surface of a 5-sphere in six-dimensional space are equivalent to the 27 lines that describe a general cubic surface.6 The three-space projction of a portion of this 27-line figure is called a Schlafli Double-Six, and it has the overall symmetry of the tetrahedron. Any flus to or from a hyperdimensional vacuum that takes place according to this model should reveal itself with a tetrahedral pattern. (See Figure 2.)
Richard Hoagland has pointed out that the Sun and many planets display phenomena taking place according to tetrahedral geometry.8 A circumscribed tetrahedron having one vertex located at a pole will have the other vertices tracing a line of latitude at 19.5°. The phenomena in question take the form of energetic upwellings that occur preferentially at 19.5° north or south. Some of these phenomena include the volcanic vent forming the Hawaiian Islands, the largest volcano on Mars – Olympus Mons, and the Great Spots of Jupiter and Neptune.
This tetrahedral energy phenomenon is especially interesting for the planet Neptune, which is radiating about 2.7 times more energy than it receives from the Sun. A possible explanation is that the rotation of Neptune is enabling a coherence to take place with the vacuum zero-point energy flux, which then assumes a form associated with projection to three-space. Alternatively, if the rotating body is itself partially residing in complexified three-space, then what would have been conventional fluid dynamics will exhibit the geometry of a phase transition between dimensionalities.
An Alternative Theory of Light
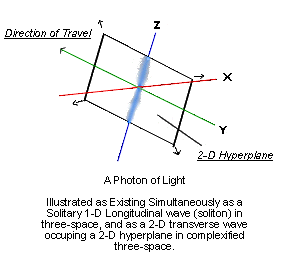
Figure 3.
Earlier, quantum electrodynamics was quoted as describing the vacuum as a region of very active virtual particle flux. The stress in this vacuum is a scalar potential, since it ordinarily has no vectors, or preferred directions. If we take the concept of light as being a longitudinal wave, we may imagine the photon as being a pulse in the vacuum. This solitary wave, or soliton, will be a region of increased scalar potential, and will be propagating at the speed of light. Recall the icosahedral model for vacuum geometry. If this soliton's passage through the vacuum is accompanied by an orthorotation into a higher dimensional space, the forward direction of the soliton at this point will experience an orthorotation into a complex plane. The 1-D longitudinal soliton will then be free to exist, at the same time, as a 2-D transverse wave that occupies this complex plane. The 1-D longitudinal soliton represents the "particle" nature of light, and the 2-D transverse wave represents the "wave" nature. This suggests an origin for the wave-particle duality of light. Light can have a wave and a particle nature simultaneously if these two traits of light occupy space of differing dimensionality. (See Figure 3.)
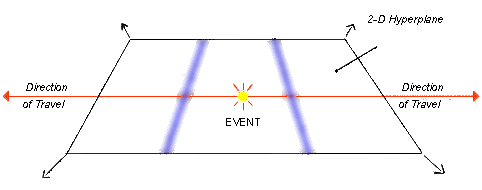
Since the distance a photon will travel in three-space is indeterminate, the extent of this complex plane should also be indeterminate. The idea that a photon may partially exist on a 2-D hyperplane in complexified three-space may provide an explanation for the results of the "double slit" experiment, where a photon appears to be able to pass through two holes simultaneously. It may also explain the experiment performed by Alain Aspect in 1982 at the University of Paris. In the Aspect experiment, two photons were created by a single event and guided through separate optical paths. Each photon "knew" the polarization of its partner, even though the two photons were far enough apart that a signal at the speed of light could not have passed between them. Since no known physical process could explain this connectivity, the two photons were said to be non-locally connected. If these two photons shared a common 2-D hyperplane in complexified three-space, this may provide a mechanism for this non-local connection. (See Figure 4.)
Figure 4.
Non-Local Connectivity
In the Aspect experiment, a single event creates two photons that are non-locally connected and aware of each other's polarization state. This is possible in a complexified æther if the two photons share a common 2-D hyperplane.
Conclusion
If the above speculations on vacuum geometry are correct, then each
orthogonal turn into an adjacent hyperspace will be governed by the Golden
Section proportion. This should prove experimentally useful to those attempting
to design and construct resonant systems that would connect our three-dimensional
reality with the hyperdimensional reality of the vacuum state.
1J.A. WHeeler, Geometrodynamics,
Academic Press, N.Y., 1962.
2Moray B. King, Tapping
the Zero-Point Energy, Paraclete Publishing, Utah, 1989, p. 130-134
3Rho Sigma, Ether-Technology,
Cadake Industries, 1986, p. 73-80
4Peter W. Stevens
and Alan I. Goldman, The Structure of Quasicrystals, Scientific
American, April 1991, p. 44-53
5P. Bak, Icosahedral
Crystals: Where Are the Atoms?, Phys. Rev. Lett., 56, 8, p. 861-864
(1986)
6H.S.M. Coxeter, The
Polytope 2,21, Whose Twenty-Seven Vertices Correspond to the Lines on the
General Cubic Surface, American Journal of Mathematics, v62, 1940,
p. 457-486
7S. Tenen, Meru
Foundation Technical Update February 1993: The 27-Lines that Solve the
General Cubic Equation, Schlafli's Double-6, Hyperspheres, and Tori,
32-minute videotape demonstration ©1993 Stan Tenen
8Richard C. Hoagland, The Monuments of Mars: A City on the Edge of Forever, North Atlantic
Books, ©1992 R. Hoagland, p. 352-355.
Meru Foundation, 524 San Anselmo Ave. #214, San Anselmo, CA 94960.
Email inquiries to: meru@meru.org